Um canteiro com formato retangular tem área igual a 40 m2 e sua diagonal mede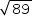 
m. O perímetro desse retângulo é:
Sendo a e b as dimensões do canteiro retangular, considere-se a figura a seguir:
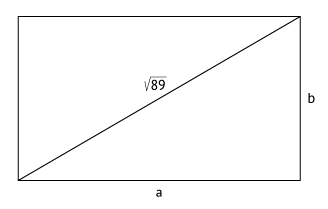
Aplicando-se o teorema de Pitágoras no triângulo retângulo, tem-se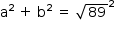 
, ou seja, a2 + b2 = 89. (I)
Como a área do canteiro vale 40, tem-se que ab = 40 e, assim, 2ab = 80. (II)
Somando-se, membro a membro, as equações (I) e (II), tem-se:
a2 + 2ab + b2 = 89 + 80
(a + b)2 = 169
Como a e b são números positivos, tem-se a + b = 13 e, portanto, o perímetro desse retângulo é dado por 2a + 2b = 2(a + b) = 2 · 13 = 26 m.