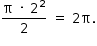A primeira inequação corresponde ao círculo de centro na origem e raio de medida 2. Já a segunda inequação descreve a região abaixo da bissetriz dos quadrantes pares, contendo a própria bissetriz.

Assim, tem-se a figura na qual a região destacada representa a intersecção das regiões apresentadas:

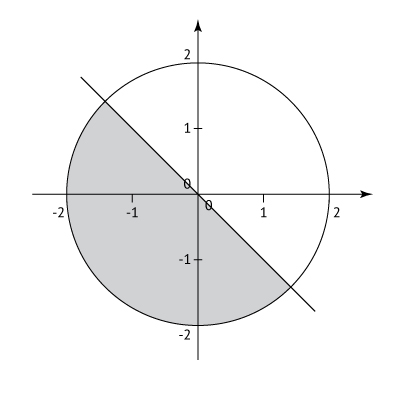
Logo, a área da região determinada pelas inequações pode ser calculada fazendo-se a metade da área do círculo de raio de medida 2, ou seja,