Um fazendeiro dispõe de material para construir 60 metros de cerca em uma região retangular, com um lado adjacente a um rio.
Sabendo que ele não pretende colocar cerca no lado do retângulo adjacente ao rio, a área máxima da superfície que conseguirá cercar é:
Como o fazendeiro não pretende colocar cerca no lado do retângulo adjacente ao rio, podemos representar a região pela figura abaixo, em que x e y são as dimensões indicadas:
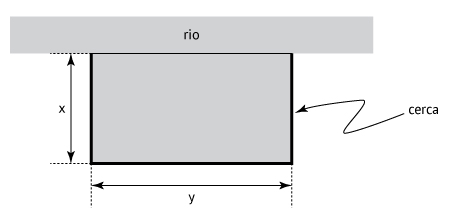
Do enunciado, tem-se que 2x + y = 60 
y = − 2x + 60.
A área A do retângulo obtido é dada por
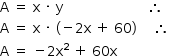
O valor máximo de A é dado por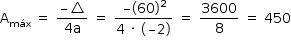 
. Logo, a área máxima da superfície que o fazendeiro conseguirá cercar é 450 m2.