Os pares(y,x) dados abaixo pertencem a uma reta (r) do plano cartesiano:
Podemos afirmar que
- a
a reta (r) intercepta o eixo das abscissas no ponto de abscissa – 4.
- b
o coeficiente angular da reta (r) é – 5.
- c
a reta (r) determina com os eixos cartesianos um triângulo de área 1,6.
- d
y será positivo se, e somente se, x >
. - e
A reta (r) intercepta o eixo das ordenadas no ponto de abscissa
.
A reta (r) passa pelos pontos (– 4, – 24) e (– 2, – 14); logo, seu coeficiente angular m é dado por:
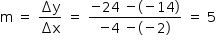
A reta r passa pelo ponto (0, – 4); logo, seu coeficiente linear é – 4 . Assim, sua equação reduzida é y = 5x – 4.
Graficamente, tem-se:
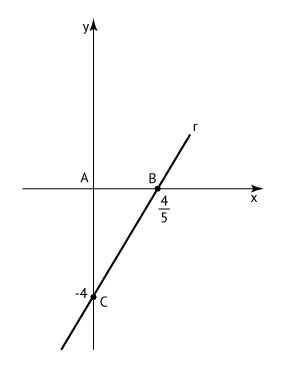
A área S do triângulo que a reta (r) determina com os eixos cartesianos é dada por:
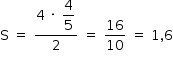
Pode-se demonstrar que as demais alternativas não são corretas.
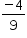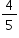