A - De forma consecutiva extraímos de uma urna três bolas numeradas de 1 a 9, repondo a bola retirada após cada extração, formando um número de três algarismos. O primeiro algarismo sorteado é o algarismo das centenas; o segundo, o das dezenas; e o terceiro, o das unidades. Calcule a probabilidade de que saia um número
I - com três algarismos repetidos;
II - sem nenhum algarismo repetido;
III - com exatamente dois algarismos exatamente iguais.
B - Em uma caixa com 10 lapiseiras, 4 delas estão com defeito. Se um cliente compra 2 lapiseiras escolhidas aleatoriamente, é certo afirmar que a probabilidade de que nenhuma lapiseira esteja com defeito é maior que 30%?
A)
I. A probabilidade de que saia um número com três algarismos repetidos é dada por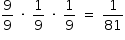 
;
II. A probabilidade de que saia um número sem algarismos repetidos é dada por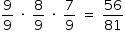 
;
III. O experimento proposto resulta em apenas três possibilidades: três algarismos repetidos (item I, probabilidade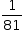 
), sem algarismos repetidos (item II, probabilidade 
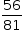) e com exatamente dois algarismos repetidos (item III, probabilidade p). Segue, portanto, que a soma dessas probabilidades resulta em 1:
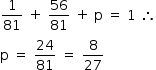
Respostas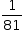: I. ; II. 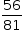; III.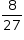 
B)
Se, na caixa com 10 lapiseiras, 4 delas estão com defeito, pode-se admitir que as outras 6 lapiseiras não apresentam defeito. Logo, na compra de duas lapiseiras, a probabilidade de que nenhuma lapiseira esteja com defeito é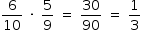 
. Como 
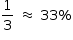, conclui-se que é correto afirmar que esta probabilidade é maior do que 30%.
Resposta: Sim, é correto.