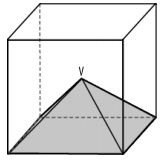
A - O volume do cubo da figura é 64 cm³. O ponto V é o ponto de encontro das diagonais do cubo. Qual é o volume da pirâmide de vértice V?
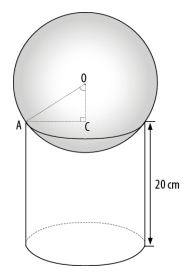
B - Uma bola de vidro que é uma esfera de centro O se encaixou num copo exatamente como mostra a figura. O raio da bola mede 13 cm e OC = 5 cm. O segmento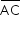 
é o raio do cilindro. O que tem o maior volume: a bola ou o copo?
A) Seja L a medida da aresta do cubo. Como seu volume vale 64 cm3, deve-se ter:
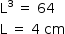
O ponto V é o encontro das diagonais do cubo; assim, tem-se que a distância desses ponto ao plano da base da pirâmide vale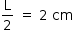 
. A partir disso, o volume V da pirâmide é dado por:
B) A partir do enunciado, tem-se a seguinte figura:
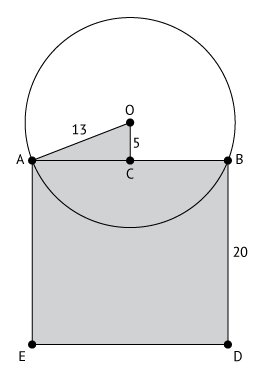
Do triângulo retângulo AOC, tem-se:
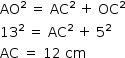
A partir disso, tem-se:
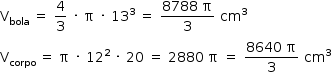
Como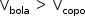 
, o sólido de maior volume é a bola.
Resposta: A bola.