A - Sabendo que x é um inteiro e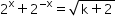 
podemos afirmar que 4x + 4-x? Justifique a sua resposta.
B - Se x e y são dois números reais positivos, x < y e xy = 121, podemos afirmar que x <11< y? Justifique a sua resposta.
A)
Sabendo-se que x é um inteiro e que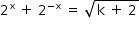 
, tem-se:
Ou seja, pode-se afirmar que 4x + 4-x = k.
Resposta: Sim
B)
Tem-se que 121 = 11 · 11. Assim, se 121 for escrito como um produto de dois fatores, tem-se que ambos os fatores são iguais a 11 ou, se um dos fatores for menor que 11, o outro deverá ser maior que 11 (já que o produto de dois fatores menores que 11 resultaria em um número menor que 121).
Como 121 = xy e x < y, deve-se ter x < 11 e y > 11, ou seja, pode-se afirmar que x < 11 < y.
Resposta: Sim