A - Determinar a soma dos 20 primeiros termos da sequência (a1, a2, ..., an, ...) definida por: an = 2 + 4n se n é ímpar e an = 4 + 6 se n é par.
B - Considere a sequência (1,10,11, ...,19,100,101,...,199,...) formada por todos os números naturais que têm 1 como primeiro algarismo no sistema decimal de numeração, tomados em ordem crescente. Se a soma dos seus n primeiros termos é 347, qual é o valor de n e o valor numérico de an?
A) A soma dos 20 primeiros termos pode ser separada da seguinte maneira:
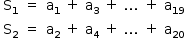
Assim, tem-se que:
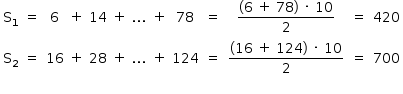
Com isso, a soma dos 20 primeiros termos da sequência é dada por:
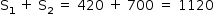
Resposta: 1120
B) Separe-se a soma em três partes, T1, T2 e T3, de acordo com o número de algarismos de cada número:
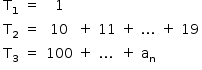
Note-se que é impossível que T3 tenha sua soma composta de mais de 3 valores, já que, a partir de 4 termos, a soma já ultrapassaria os 347.
Além disso, tem-se que:
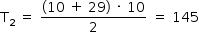
Com isso, chega-se a:
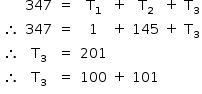
Dessa forma, tem-se que a soma foi feita até os dois primeiros números com três algarismos, o que significa que, junto com os outros 11 números, foram somados um total de n = 13 números.
Resposta: n = 13 e a13 = 101.