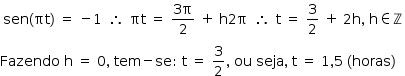Uma quantidade fixa de um gás ideal é mantida a temperatura constante, e seu volume varia com o tempo de acordo com a seguinte fórmula:
V(t) = log2(5 + 2 sen(πt)), 0 ≤ t ≤ 2,
em que t é medido em horas e V (t) é medido em m³. A pressão máxima do gás no intervalo de tempo [0,2] ocorre no instante
Como a temperatura é constante, tem-se que pressão e volume são grandezas inversamente proporcionais. Então a pressão será máxima quando o volume for mínimo.
O volume em função do tempo é dado por
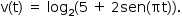
Como a base do logaritmo é 2, o menor valor de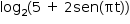 
ocorre quando 5 + 2sen(πt) for mínimo. Assim, tem-se:
