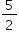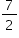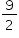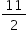Duas circunferências com raios 1 e 2 têm centros no primeiro quadrante do plano cartesiano e ambas tangenciam os dois eixos coordenados. Essas circunferências se interceptam em dois pontos distintos de coordenadas (x1, y1) e (x2, y2).
O valor de (x1 + y1)² + (x2 + y2)² é igual a
- a
- b
- c
- d
- e
Como as circunferências têm centros no primeiro quadrante e são tangentes aos eixos, seus centros são da forma (r, r), em que r é a medida do raio da circunferência. Logo, tem-se:
- Sendo λ1 a circunferência de centro (1, 1) e raio 1, sua equação é dada por (x – 1)2 + (y – 1)2 = 1, ou seja, x2 + y2 – 2x – 2y + 1 = 0;
- Sendo λ2 a circunferência de centro (2, 2) e raio 2, sua equação é dada por (x – 2)2 + (y – 2)2 = 4, ou seja, x2 + y2 – 4x – 4y + 4 = 0.
Os pontos (x1, y1) e (x2, y2) são soluções do sistema:
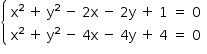
Subtraindo as equações, tem-se 2x + 2y – 3 = 0, ou seja,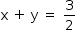 
. Logo,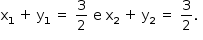 
Assim, o valor de (x1 + y1)2 + (x2 + y2)2 é dado por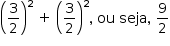 
.