O polinómio P(x) = x³ - 3x² + 7x - 5 possui uma raiz complexa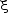 
cuja parte imaginária é positiva. A parte real de 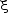³ é igual a
Do polinômio P(x) = x3 – 3x2 + 7x – 5, tem-se que P(1) = 0; logo, 1 é raiz.
Aplicando-se Briot-Ruffini:
,
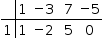tem-se a equação x2 – 2x + 5 = 0, cujas raízes são 1 – 2i e 1 + 2i.
Do enunciado, tem-se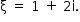 
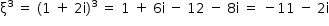
Portanto, a parte real de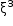 
é –11.