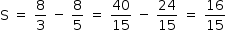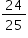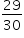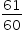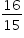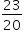Na figura, o retângulo ABCD tem lados de comprimento AB = 4 e BC = 2. Sejam M o ponto médio do lado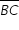 
e N o ponto médio do lado 
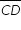. Os segmentos 
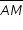e 
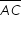interceptam o segmento 
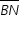nos pontos E e F, respectivamente.
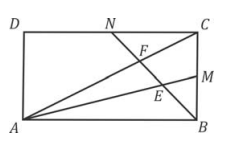
A área do triângulo AEF é igual a
- a
- b
- c
- d
- e
Considere as figuras a seguir:
Figura I:
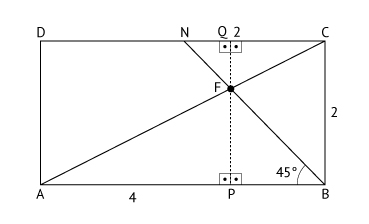
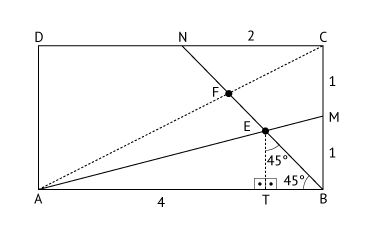
Figura II:
Na figura I, sendo h = PF, tem-se QF = 2 – h. Como os triângulos AFB e CFN são semelhantes,
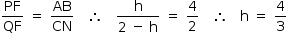
Logo, a área do triângulo AFB é dada por:
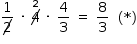
Considere, agora, a figura II.
Sendo h' = ET, tem-se, do triângulo isósceles ETB, que TB = h'. Ainda, da semelhança dos triângulos AET e AMB: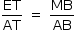 
Logo,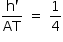 
e, assim, AT = 4h'. Como AT + TB = 4, tem-se 4h' + h' = 4 e, dessa forma, 
.
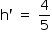Assim, a área do triângulo AEB é dada por:
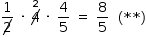
A área S pedida do triângulo AEF pode ser dada subtraindo-se a área do triângulo AEB da área do triângulo AFB. Logo, a partir de (*) e (**), vem que:
