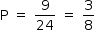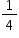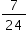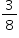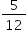Cláudia, Paulo, Rodrigo e Ana brincam entre si de amigo-secreto (ou amigo-oculto). Cada nome é escrito em um pedaço de papel, que é colocado em uma urna, e cada participante retira um deles ao acaso. A probabilidade de que nenhum participante retire seu próprio nome é
Cada retirada de papel pode ser representada por uma sequência de 4 letras. O total de sequências possíveis é dado por 4! = 24.
Sendo A, P, C, R as letras que representam os nomes Ana, Paulo, Cláudia e Rodrigo, respectivamente, temos que a sequência (A, P, C, R) representa cada participante retirar o seu próprio nome.
Das 24 sequências possíveis, os casos em que nenhum deles retira o seu próprio nome são: (P, A, R, C), (C, A, R, P), (R, A, P, C), (P, C, R, A), (C, R, A, P), (R, C, A, P), (P, R, A, C), (C, R, P, A), (R, C, P, A).
Logo, a probabilidade de que nenhum deles retire o seu próprio nome é dada por: