João tem R$ 150,00 para comprar canetas em 3 lojas. Na loja A, as canetas são vendidas em dúzias, cada dúzia custa R$ 40,00 e há apenas 2 dúzias em estoque. Na loja B, as canetas são vendidas em pares, cada par custa R$ 7,60 e há 10 pares em estoque. Na loja C, as canetas são vendidas avulsas, cada caneta custa R$ 3,20 e há 25 canetas em estoque. O maior número de canetas que João pode comprar nas lojas A, B e C utilizando no máximo R$ 150,00 é igual a
Seja x a quantidade de dúzias de canetas compradas em A; y, a quantidade de pares comprados em B; e z, a quantidade de unidades compradas em C. Dessa forma, compra-se um total de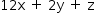 
canetas por 
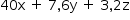reais, com 
.
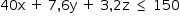Supondo que x tenha sido determinado de modo que as quantidades y e z ainda sejam desconhecidas, enquanto houver pares de canetas disponíveis tanto em B quanto em C, certamente é mais vantajoso comprar um par em C, já que nessa loja as canetas são mais baratas. Assim, determinado o valor de x, segue que o valor de z deve ser máximo, desde que haja pares disponíveis em B e C.
Dessa forma, é preciso analisar as três possibilidades para x: x = 0, x = 1 ou x = 2.
1º caso: x = 0
Deve-se ter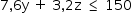 
O maior valor possível para z de modo que ainda sobre um par de canetas em C é z = 23. Logo, deve-se considerar z = 24 ou z = 25.
Com z = 24, tem-se y = 9 e um total de 42 canetas;
com z = 25, tem-se y = 9 e um total de 43 canetas.
2º caso: x = 1
Deve-se ter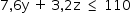 
Novamente, deve-se considerar z = 24 ou z = 25.
Com z = 24, tem-se y = 4 e um total de 44 canetas;
com z = 25, tem-se y = 3 e um total de 43 canetas.
3º caso: x = 2
Deve-se ter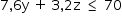 
O maior valor possível é z = 21, caso em que ainda sobram pares na loja C. Logo, é o único caso a ser considerado e tem-se y = 0, stituação em que a quantidade total de canetas compradas é 45, o maior valor possível.