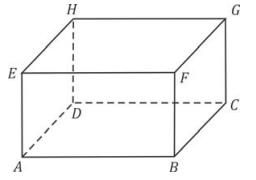
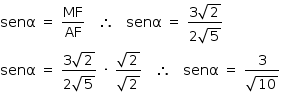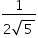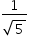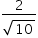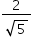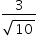O paralelepípedo reto-retângulo ABCDEFGH, representado na figura, tem medida dos lados AB = 4, BC = 2 e BF = 2.
O seno do ângulo HÂF é igual a
Do enunciado, tem-se a figura abaixo:
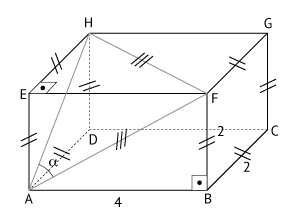
No triângulo retângulo ABF:
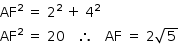
No triângulo retângulo EFH:
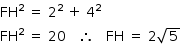
No triângulo retângulo AEH:
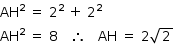
Assim, tem-se o triângulo isósceles abaixo:
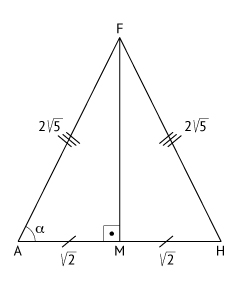
No triângulo retângulo AMF:
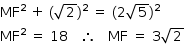
Sendo α a medida do ângulo HÂF: