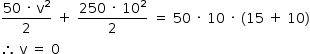Helena, cuja massa é 50 kg, pratica o esporte radical bungee jumping. Em um treino, ela se solta da beirada de um viaduto, com velocidade inicial nula, presa a uma faixa elástica de comprimento natural L0 = 15 m e constante elástica k = 250 N/m. Quando a faixa está esticada 10 m além de seu comprimento natural, o módulo da velocidade de Helena é
Note e adote:
Aceleração da gravidade: 10 m/s².
A faixa é perfeitamente elástica; sua massa e efeitos dissipativos devem ser ignorados.
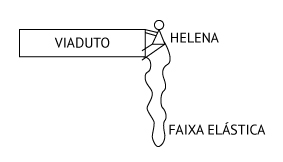
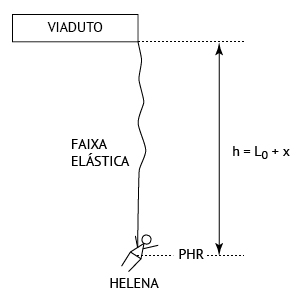
A situação descrita pelo enunciado pode ser esquematizada como segue:
Situação inicial
Situação final
Segundo o enunciado, o sistema é conservativo. Logo:
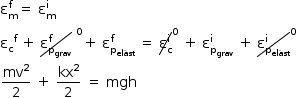
Substituindo-se os dados do enunciado, tem-se: