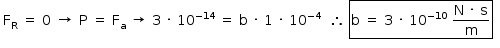Objetos em queda sofrem os efeitos da resistência do ar, a qual exerce uma força que se opõe ao movimento desses objetos, de tal modo que, após um certo tempo, eles passam a se mover com velocidade constante. Para uma partícula de poeira no ar, caindo verticalmente, essa força pode ser aproximada por 
, sendo 
a velocidade da partícula de poeira e b uma constante positiva. O gráfico mostra o comportamento do módulo da força resultante sobre a partícula, FR, como função de v, o módulo de .
O valor da constante b, em unidades de N • s/m, é
As forças que atuam na partícula são a força peso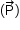 
e a força de resistência do ar 
.
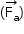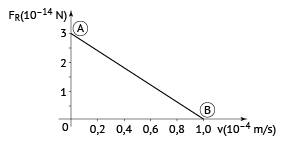
O gráfico destacado expressa a intensidade da resultante das forças aplicadas na partícula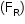 
em função da velocidade.
No ponto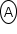 
, como a velocidade é zero, a intensidade da força de resistência do ar 
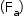é nula, assim a intensidade da resultante é igual à intensidade da força peso (P).
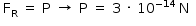
No ponto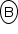 
, a intensidade da resultante é zero; portanto, a intensidade da força peso é igual à intensidade da força de resistência do ar.
