A figura foi obtida em uma câmara de nuvens, equipamento que registra trajetórias deixadas por partículas eletricamente carregadas. Na figura, são mostradas as trajetórias dos produtos do decaimento de um isótopo do hélio (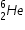
) em repouso: um elétron (e-) e um isótopo de lítio (
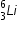), bem como suas respectivas quantidades de movimento linear, no instante do decaimento, representadas, em escala, pelas setas. Uma terceira partícula, denominada antineutrino (
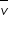, carga zero), é também produzida nesse processo.
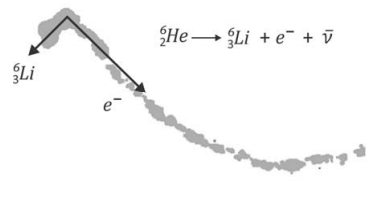
O vetor que melhor representa a direção e o sentido da quantidade de movimento do antineutrino é
- a
- b
- c
- d
- e
A situação analisada é o decaimento radioativo de um isótopo de Hélio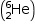 
.
Por hipótese, as partículas envolvidas em decaimentos como esse constituem um sistema isolado, logo:
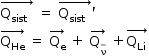
De acordo com o enunciado, o átomo de hélio estava em repouso, então:
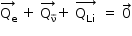
Para que essa soma vetorial seja nula, a quantidade de movimento do antineutrino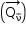 
deve ser:
