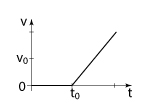
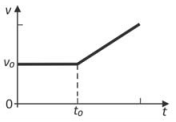
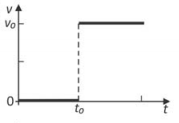
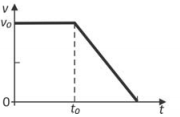
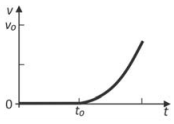
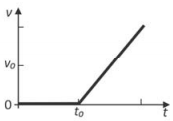
Um elevador sobe verticalmente com velocidade constante v0, e, em um dado instante de tempo t0, um parafuso desprende-se do teto. O gráfico que melhor representa, em função do tempo t, o módulo da velocidade v desse parafuso em relação ao chão do elevador é
Note e adote:
Os gráficos se referem ao movimento do parafuso antes que ele atinja o chão do elevador.
Dado que:
- Enquanto o parafuso se encontra preso ao teto, a velocidade relativa
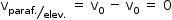
- A partir do instante t0, o parafuso ficará sujeito exclusivamente à ação do peso. Assim, até o instante em que o parafuso atinge o chão do elevador
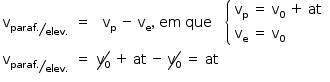
logo, o gráfico que melhor representa a situação é: