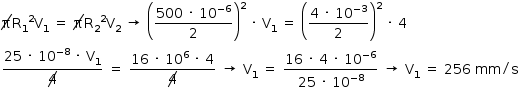A microfluídica é uma área de pesquisa que trabalha com a manipulação precisa de líquidos em canais com dimensões submilimétricas, chamados de microcanais, possibilitando o desenvolvimento de sistemas miniaturizados de análises químicas e biológicas. Considere que uma seringa com êmbolo cilíndrico de diâmetro D = 4 mm seja usada para injetar um líquido em um microcanal cilíndrico com diâmetro de d = 500 μm. Se o êmbolo for movido com uma velocidade de V = 4 mm/s, a velocidade v do líquido no microcanal será de
Como o volume transferido da seringa para o microcanal por unidade de tempo é o mesmo, encontra-se a seguinte relação:
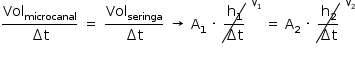
A1 · V1 = A2 · V2 (Equação da continuidade)