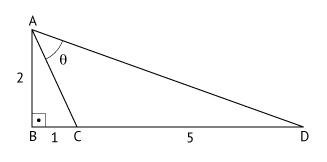
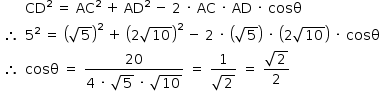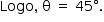Considere o triângulo retângulo ABC exibido na figura abaixo, em que AB = 2 cm, BC = 1 cm e CD = 5 cm. Então, o ângulo θ é igual a
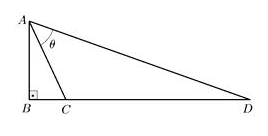
Da figura dada no enunciado, tem-se:
Aplicando-se o Teorema de Pitágoras nos triângulos retângulos ABC e ABD, tem-se:
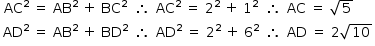
Aplicando-se o Teorema dos Cossenos no triângulo ACD, tem-se: