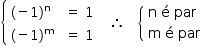Considere o polinômio p(x) = xn + xm + 1, em que n > m ≥ 1. Se o resto da divisão de p(x) por x + 1 é igual a 3, então
Do teorema do resto, tem-se:
p(-1) = 3
Como p(x) = xn + xm + 1,
p(–1) = (–1)n + (–1)m + 1 = 3.
Para que a soma acima resulte em 3, deve-se ter: