Sabe-se que, em um grupo de 10 pessoas, o livro A foi lido por 5 pessoas e o livro B foi lido por 4 pessoas. Podemos afirmar corretamente que, nesse grupo,
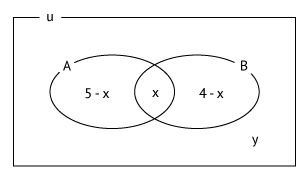
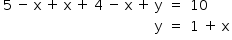
Como 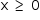 , tem-se que
, tem-se que 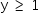 .
.
Logo, pelo menos uma pessoa não leu nenhum dos dois livros.
Sabe-se que, em um grupo de 10 pessoas, o livro A foi lido por 5 pessoas e o livro B foi lido por 4 pessoas. Podemos afirmar corretamente que, nesse grupo,

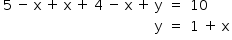
Como 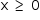 , tem-se que
, tem-se que 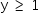 .
.
Logo, pelo menos uma pessoa não leu nenhum dos dois livros.