Em uma aula de geometria, o professor passou a seguinte instrução:
Desenhe um retângulo de lados 8 cm por 14 cm. Nomeie os vértices desse retângulo de A, B, C e D, sendo que AB deve ser um dos menores lados. Determine o ponto médio do lado AB e nomeie esse ponto pela letra M. A partir do ponto M trace um segmento paralelo aos lados maiores e que tenha 3 cm de comprimento. Nomeie esse segmento de MN. Determine a área do triângulo NCD.
Natália e Mariana seguiram as instruções dadas, porém chegaram a resultados diferentes. Se o professor considerou correta as duas resoluções, a diferença, em cm2, entre as áreas obtidas por Natália a Mariana foi
Do enunciado, tem-se a figura, cotada em cm, exibindo duas possibilidades para o ponto N, no interior ou no exterior do retângulo ABCD:
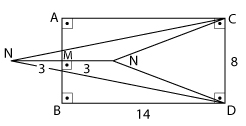
Observa-se, da figura, que o triângulo NCD tem base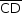 
medindo 8 cm, e a altura relativa a essa base pode medir:
- 14 – 3 = 11 cm, caso N esteja no interior do retângulo;
- 14 + 3 = 17 cm, caso N esteja no exterior do retângulo.
Assim, a diferença entre as áreas é dada por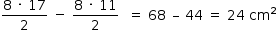 
.