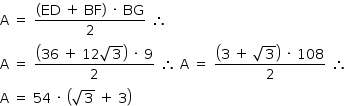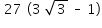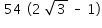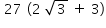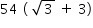Os pontos B e F são extremidades da circunferência de equação x2 + y2 = 81 e o segmento DE é tangente à circunferência dada no ponto C(0, 9).
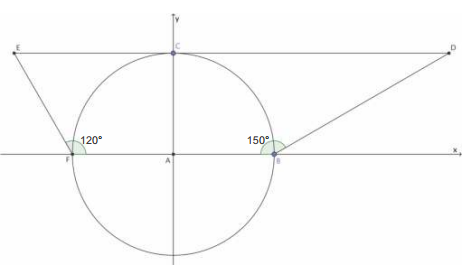
No trapézio BDEF o ângulo F mede 120º e o ângulo B mede 150º, conforme mostra a figura. A área do trapézio BDEF vale
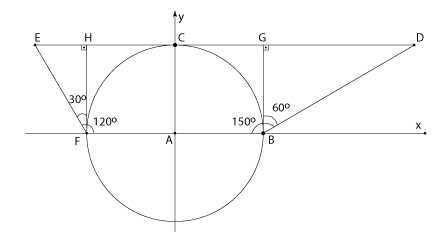
Do enunciado, o raio da circunferência mede 9; assim, entendendo-se que B e F são extremidades de um diâmetro da circunferência, tem-se BF = 18, GH = 18 e, ainda, BG = FH = 9. Logo:
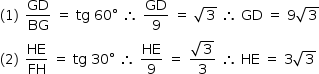
Como ED = HE + GH + GD, de (1), (2) e GH = 18, tem-se ED = 18 + 12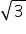
Sendo A a área do trapézio BDEF, chega-se a: