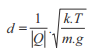Observe a figura abaixo onde duas esferas de massas iguais a m estão eletrizadas com cargas elétricas Q, iguais em módulo, porém de sinais contrários. Estando o sistema em equilíbrio estático, determine a distância d entre os centros das esferas. Adote o módulo da aceleração da gravidade igual a g, a constante eletrostática do meio igual a k e a tração na corda igual a T.
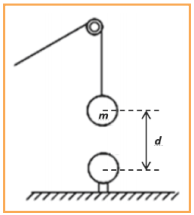
Na condição de equilíbrio estático, a resultante é nula sobre a esfera superior, que está submetida à força de tração (T), à força gravitacional (P = mg) e à força elétrica (Fe).
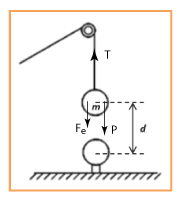
Em módulo, tem-se: