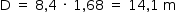Na modalidade esportiva do salto à distância, o esportista, para fazer o melhor salto, deve atingir a velocidade máxima antes de saltar, aliando-a ao melhor ângulo de entrada no momento do salto que, nessa modalidade, é o 45 . Considere uma situação hipotética em que um atleta, no momento do salto, alcance a velocidade de 43,2 km/h, velocidade próxima do recorde mundial dos 100 metros rasos, que é de 43,9 km/h. Despreze o atrito com o ar enquanto ele está em “vôo” e considere o saltador como um ponto material situado em seu centro de gravidade. Nessas condições, qual seria, aproximadamente, a distância alcançada no salto?
Adote o módulo da aceleração da gravidade igual a 10 m/s2.
Dados: sen45º = cos45º = 0,7

https://sites.google.com/site/edfisicaempic/educacao-fisica-corpo-e-mente/atletismo
No momento inicial do salto, a velocidade inicial, no SI, é de 12 m/s (43,2 km/h). Como o ângulo de lançamento é de 45o, as componentes horizontal e vertical da velocidade são iguais entre si e valem 8,4 m/s.
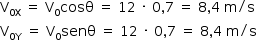
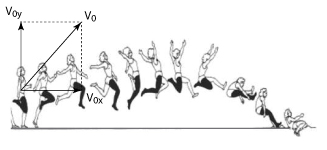
Desprezando-se a altura inicial do centro de gravidade do atleta, as funções horárias de movimento – para a componente da velocidade vertical e para o alcance horizontal, adotando a origem do sistema coordenado na posição inicial do centro de gravidade – são:
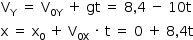
No ponto mais alto da trajetória, a velocidade vertical é nula.
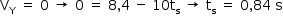
Essa condição determina um tempo de subida igual a 0,84 s. Como o tempo de subida é igual ao tempo de descida, tem-se um tempo de voo de 1,68 s.
Dessa forma, o alcance máximo do salto, dado pela função horária x(t) calculada para o tempo de voo: