Para uma feira de ciências, dois projéteis de foguetes, A e B, estão sendo construídos para serem lançados. O planejamento é que eles sejam lançados juntos, com o objetivo de o projétil B interceptar o A quando esse alcançar sua altura máxima. Para que isso aconteça, um dos projéteis descreverá uma trajetória parabólica, enquanto o outro irá descrever uma trajetória supostamente retilínea. O gráfico mostra as alturas alcançadas por esses projéteis em função do tempo, nas simulações realizadas.
Com base nessas simulações, observou-se que a trajetória do projétil B deveria ser alterada para que o objetivo fosse alcançado.
Para alcançar o objetivo, o coeficiente angular da reta que representa a trajetória de B deverá
Originalmente, a trajetória do projétil B passa pelos pontos (0, 0) e (2, 4), como visto no gráfico. Logo, seu coeficiente angular é:
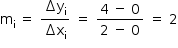
Como a trajetória do projétil B deve encontrar a trajetória do projétil A em sua altura máxima, o projétil B deve partir da origem (0, 0) e passar pelo ponto (4, 16), no qual A tem sua altura máxima. Logo, o coeficiente angular será:
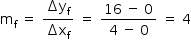
A diferença entre ambos os coeficientes é, portanto, de:
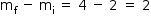
Ou seja, deve aumentar em 2 unidades.