Um dos grandes desafios do Brasil é o gerenciamento dos seus recursos naturais, sobretudo os recursos hídricos. Existe uma demanda crescente por água e o risco de racionamento não pode ser descartado. O nível de água de um reservatório foi monitorado por um período, sendo o resultado mostrado no gráfico. Suponha que essa tendência linear observada no monitoramento se prolongue pelos próximos meses.
Nas condições dadas, qual o tempo mínimo, após o sexto mês, para que o reservatório atinja o nível zero de sua capacidade?
Adaptando-se o gráfico para ter os eixos passando pela origem (0, 0), obtém-se:
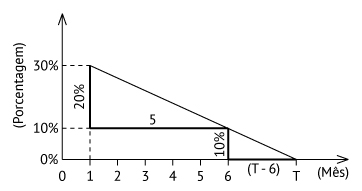
Seja T o mês em que o reservatório atingiria 0% da capacidade total.
Então, desse gráfico, tem-se:
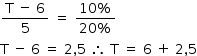
Logo, para que o nível do reservatório atinja o nível zero, serão necessários 2,5 meses após o sexto mês.