Uma família resolveu comprar um imóvel num bairro cujas ruas estão representadas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal. Desconsidere a largura das ruas.
A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A.
Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas
O imóvel em questão deverá estar na mediatriz do segmento de extremos no trabalho da mãe e no consultório do pai, isto é, deverá estar na rua 4.
Seja o imóvel na rua 4 e a x quadras acima da rua E. Assim:
A distância do imóvel ao consultório é dada por 2 + x.
A distância do imóvel à escola é dada por 4 – x.
Logo, para que seja equidistante, tem-se:
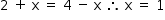
Assim, o imóvel tem de estar 1 quadra acima da rua E.
Portanto, o imóvel estará no encontro da rua 4 com a rua D.