É comum os artistas plásticos se apropriarem de entes matemáticos para produzirem, por exemplo, formas e imagens por meio de manipulações. Um artista plástico, em uma de suas obras, pretende retratar os diversos polígonos obtidos pelas intersecções de um plano com uma pirâmide regular de base quadrada.
Segundo a classificação dos polígonos, quais deles são possíveis de serem obtidos pelo artista plástico?
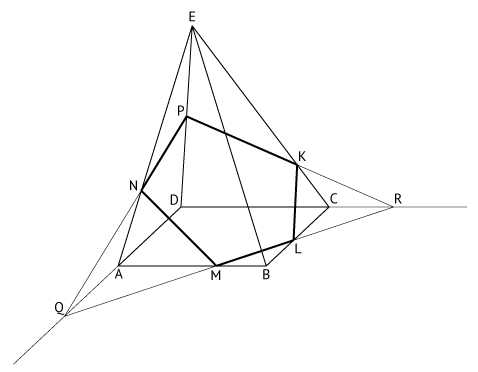
Considere a pirâmide regular de base quadrada ABCDE. A intersecção de um plano com a pirâmide pode determinar um pentágono (KLMNP).
Para provar que KLMNP é de fato plano, considere um ponto P na aresta 
, um ponto Q na semirreta 
e R na semirreta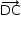 
.
P, Q e R são não colineares e determinam um plano. Como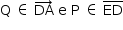 
, então 
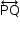está contido no plano ADE e determina N em 
.
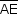Analogamente para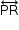 
determina-se K em 
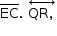por estar contida no plano da base, determina L e M nas arestas 
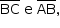respectivamente.
Logo, o pentágono KLMNP está contido no plano determinado por PQR.
Portanto, a única alternativa possível é aquela que cita pentágono.
Obs.: Os demais polígonos são de fácil visualização.