Em regiões agrícolas, é comum a presença de silos para armazenamento e secagem da produção de grãos, no formato de um cilindro reto, sobreposto por um cone, e dimensões indicadas na figura. O silo fica cheio e o transporte dos grãos é feito em caminhões de carga cuja capacidade é de 20 m3. Uma região possui um silo cheio e apenas um caminhão para transportar os grãos para a usina de beneficiamento.
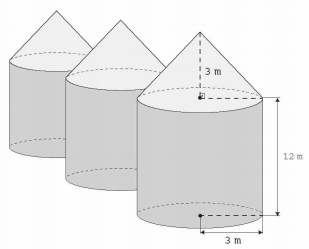
Utilize 3 como aproximação para π.
O número mínimo de viagens que o caminhão precisará fazer para transportar todo o volume de grãos armazenados no silo é
Sendo R a medida do raio do cilindro reto e do cone, H a altura do cilindro reto e h a altura do cone, tem-se que o volume (V) do silo é dado por:
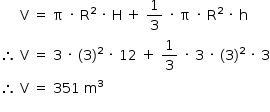
Sendo n o número de viagens do caminhão, tem-se:
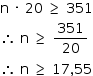
Logo, o número mínimo de viagens é 18.