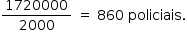Para garantir a segurança de um grande evento público que terá início às 4 h da tarde, um organizador precisa monitorar a quantidade de pessoas presentes em cada instante. Para cada 2 000 pessoas se faz necessária a presença de um policial. Além disso, estima-se uma densidade de quatro pessoas por metro quadrado de área de terreno ocupado. Às 10 h da manhã, o organizador verifica que a área de terreno já ocupada equivale a um quadrado com lados medindo 500 m. Porém, nas horas seguintes, espera-se que o público aumente a uma taxa de 120 000 pessoas por hora até o início do evento, quando não será mais permitida a entrada de público.
Quantos policiais serão necessários no início do evento para garantir a segurança?
O evento tem início às 4 h da tarde ou 16 h do dia. Portanto, deve-se contar o número de pessoas inicialmente às 10 h e quantas entrarão até às 16 h.
Sabendo-se que às 10 h o terreno ocupado equivale à área de um quadrado de lado 500 m, tem-se uma área de 5002 = 250000 m2.
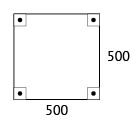
Como a densidade estimada de pessoas é de 4 por m2, a quantidade inicial será de:
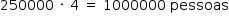
O público aumenta a uma taxa de 120000 por hora e passam-se 6 horas. Assim, tem-se um adicional de 120000 · 6 = 720000 pessoas. Respeitando a proporção de 1 policial para cada 2000 pessoas, necessita-se de: