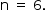Uma invenção que significou um grande avanço tecnológico na Antiguidade, a polia composta ou a associação de polias, é atribuída a Arquimedes (287 a.C. a 212 a.C.). O aparato consiste em associar uma série de polias móveis a uma polia fixa. A figura exemplifica um arranjo possível para esse aparato. É relatado que Arquimedes teria demonstrado para o rei Hierão um outro arranjo desse aparato, movendo sozinho, sobre a areia da praia, um navio repleto de passageiros e cargas, algo que seria impossível sem a participação de muitos homens. Suponha que a massa do navio era de 3 000 kg, que o coeficiente de atrito estático entre o navio e a areia era de 0,8 e que Arquimedes tenha puxado o navio com uma 
, paralela à direção do movimento e de módulo igual a 400 N. Considere os fios e as polias ideais, a aceleração da gravidade igual a 10 m/s2 e que a superfície da praia é perfeitamente horizontal.
O número mínimo de polias móveis usadas, nessa situação, por Arquimedes foi
As forças aplicadas no navio na situação de iminência de escorregamento são:
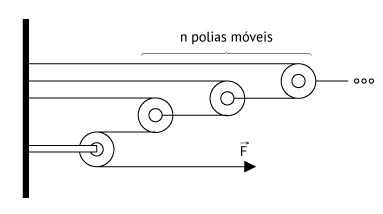
A intensidade do atrito estático máximo é dada por:
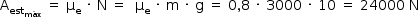
Em uma associação de polias, como mostrada na figura, com n polias móveis, a relação entre as intensidades da força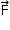 
e da força 
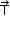é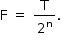 
Para que o navio inicie escorregamento, deve-se ter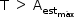 
.
Assim, considerando-se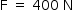 
e fazendo as devidas substituições, tem-se:
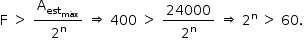
Logo, obtém-se que o valor mínimo de n que satisfaz a desigualdade acima é 