• D

    .

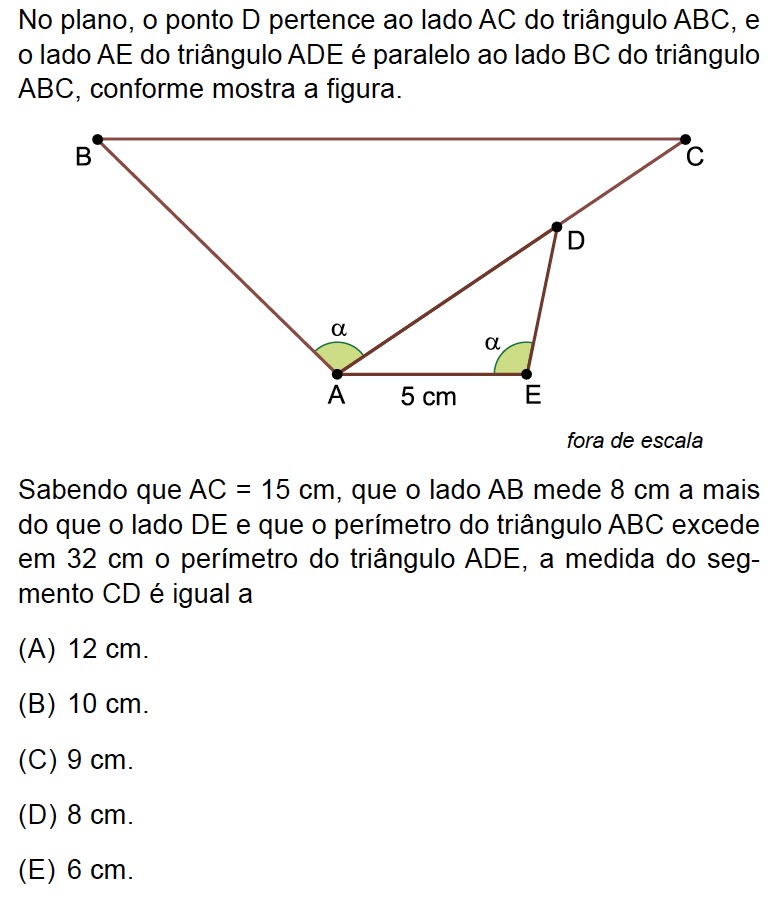
Pelo paralelismo de começar estilo tamanho matemático 14px BC em moldura superior fim do estilo com começar estilo tamanho matemático 14px AE em moldura superior fim do estilo (começar estilo tamanho matemático 14px BC em moldura superior fim do estilo // começar estilo tamanho matemático 14px AE em moldura superior fim do estilo), temos que começar estilo tamanho matemático 14px reto m parêntese esquerdo reto E reto A com conjunção lógica sobrescrito reto D parêntese direito espaço igual a espaço reto m parêntese esquerdo reto A reto C com conjunção lógica sobrescrito reto B parêntese direito igual a reto teta fim do estilo. Assim,

começar estilo tamanho matemático 14px incremento EAD semelhante incremento ACB seta dupla para a direita EA sobre AC igual a ED sobre AB igual a AD sobre CB igual a numerador 2 reto p com EAD subscrito sobre denominador 2 reto p com ACB subscrito fim da fração igual a... igual a reto k espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço então espaço espaço EA sobre AC igual a 5 sobre 15 igual a 1 terço igual a reto k fim do estilo

Do enunciado, temos que AE = ED + 8, assim:

começar estilo tamanho matemático 14px ED sobre AB igual a reto k seta dupla para a direita numerador ED sobre denominador ED mais 8 fim da fração igual a 1 terço seta dupla para a direita ED igual a 4 espaço cm fim do estilo

Usando, agora, os perímetros dos triângulos EAD e ACB, sabendo que 2pACB = 2pEAD + 32, temos:

começar estilo tamanho matemático 14px numerador 2 reto p com EAD subscrito sobre denominador 2 reto p com ACB subscrito fim da fração igual a 1 terço seta dupla para a direita 3 vezes 2 reto p com EAD subscrito igual a 2 reto p com ACB subscrito seta dupla para a direita 3 vezes 2 reto p com EAD subscrito igual a 2 reto p com EAD subscrito espaço mais 32 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço seta dupla para a direita 2 vezes 2 reto p com EAD subscrito igual a 32 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço então espaço espaço 2 com pEAD subscrito igual a 16 espaço cm fim do estilo

Sabendo o perímetro do triângulo EAD, podemos descobrir AD:

2pEAD = 16 cm  ⇒  5 + 4 + AD =  16 cm

                        então  AD = 7 cm

Como o segmento começar estilo tamanho matemático 14px CD em moldura superior fim do estilo está contido no segmento começar estilo tamanho matemático 14px AC em moldura superior fim do estilo, temos:

AC = AD + CD

então 15 = 7 + CD

então CD = 8 cm