• C

    .

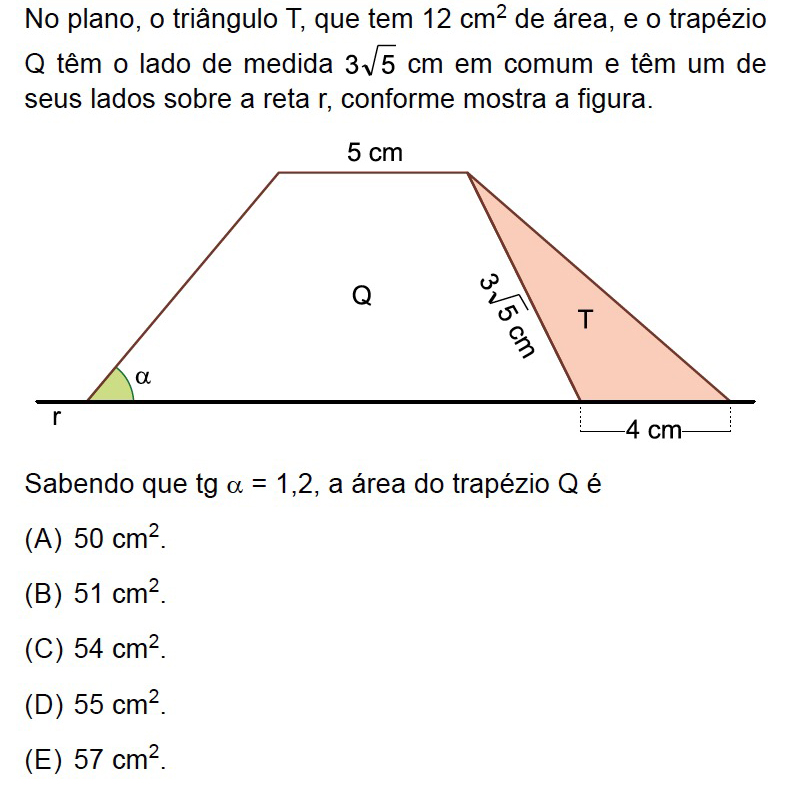
Observe a figura a seguir, onde h representa a altura do trapézio:

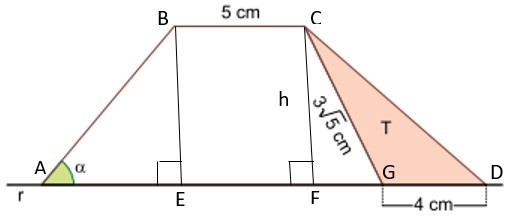
Como a área do triângulo T (ou CGD) é 12 cm2, temos que começar estilo tamanho matemático 14px numerador 4 reto h sobre denominador 2 fim da fração fim do estilo = 12  ⇔  h = 6 cm..

O triângulo CGF é retângulo em F, tem um cateto de medida 6 cm e hipotenusa começar estilo tamanho matemático 14px 3 raiz quadrada de 5 espaço cm fim do estilo, ou seja, (FG)2 = (CG)2 - (CF)2 = começar estilo tamanho matemático 14px abre parênteses 3 raiz quadrada de 5 fecha parênteses ao quadrado fim do estilo - 62 = 9  ⇔  FG = 3 cm.

.BE e CF são perpendiculares a r, logo EF = 5 cm e começar estilo tamanho matemático 14px tg reto alfa igual a BE sobre AE igual a reto h sobre AE igual a 6 sobre AE igual a 1 vírgula 2 espaço espaço seta dupla para a esquerda e para a direita espaço espaço AE espaço igual a espaço 5 espaço cm. fim do estilo.

Logo, a área do trapézio ABCG é começar estilo tamanho matemático 14px numerador parêntese esquerdo AG espaço mais espaço estreito BC parêntese direito reto h sobre denominador 2 fim da fração igual a numerador parêntese esquerdo 13 mais 5 parêntese direito 6 sobre denominador 2 fim da fração igual a 54 espaço cm ao quadrado. fim do estilo.