• B

    .

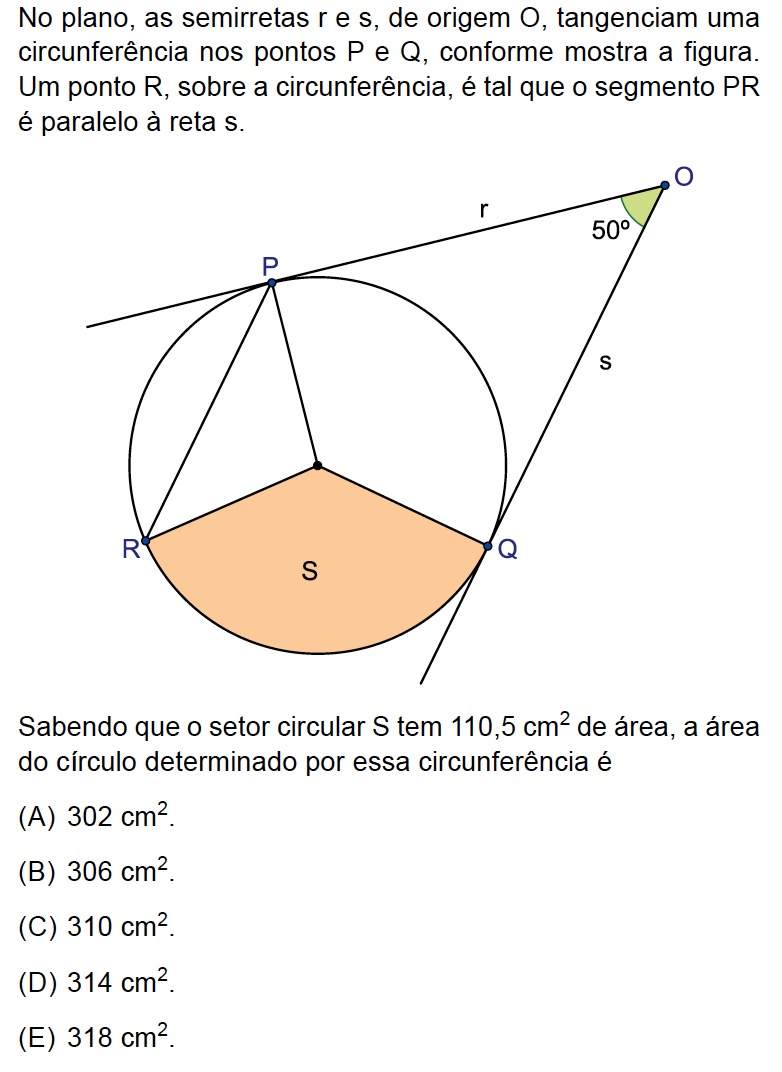
Seja A o centro da circunferência. Como as semirretas r e s são tangentes à circunferência, começar estilo tamanho matemático 14px reto m parêntese esquerdo reto A reto P com conjunção lógica sobrescrito reto O parêntese direito igual a reto m parêntese esquerdo reto A reto Q com conjunção lógica sobrescrito reto O parêntese direito igual a 90 sinal de grau fim do estilo.

Analisando os ângulos do quadrilátero APOQ, tem-se: começar estilo tamanho matemático 14px reto m parêntese esquerdo reto P reto A com conjunção lógica sobrescrito reto Q parêntese direito mais 90 sinal de grau mais 90 sinal de grau mais 50 sinal de grau igual a 360 sinal de grau espaço seta dupla para a esquerda e para a direita espaço reto m parêntese esquerdo reto P reto A com conjunção lógica sobrescrito reto Q parêntese direito igual a 130 sinal de grau fim do estilo.

Como começar estilo tamanho matemático 14px PR em moldura superior dividido por dividido por OQ em moldura superior fim do estilo, os ângulos começar estilo tamanho matemático 14px reto R reto P com conjunção lógica sobrescrito reto O fim do estilo e começar estilo tamanho matemático 14px reto P reto O com conjunção lógica sobrescrito reto Q fim do estilo são colaterais e, portanto, começar estilo tamanho matemático 14px reto m parêntese esquerdo reto R reto P com conjunção lógica sobrescrito reto O parêntese direito espaço mais espaço 50 sinal de grau igual a 180 sinal de grau espaço seta dupla para a esquerda e para a direita espaço reto m parêntese esquerdo reto R reto P com conjunção lógica sobrescrito reto O parêntese direito igual a 130 sinal de grau fim do estilo. Assim, começar estilo tamanho matemático 14px reto m parêntese esquerdo reto R reto P com conjunção lógica sobrescrito reto A parêntese direito igual a 130 sinal de grau menos 90 sinal de grau igual a 40 sinal de grau fim do estilo e, como o triângulo APR é isósceles, começar estilo tamanho matemático 14px reto m parêntese esquerdo reto P reto A com conjunção lógica sobrescrito reto R parêntese direito igual a 180 sinal de grau menos 40 sinal de grau menos 40 sinal de grau igual a 100 sinal de grau fim do estilo

Portanto, o ângulo central do setor destacado tem medida igual a 360º - 130º - 100º = 130º. Logo:

começar estilo tamanho matemático 14px abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com 130 sinal de grau seta para a direita 110 vírgula 5 espaço cm ao quadrado fim da célula linha com célula com 360 sinal de grau seta para a direita reto A com círculo subscrito fim da célula fim da tabela seta dupla para a direita espaço reto A com círculo subscrito igual a 360 sobre 130 vezes 110 vírgula 5 fecha igual a 306 espaço cm ao quadrado fim do estilo