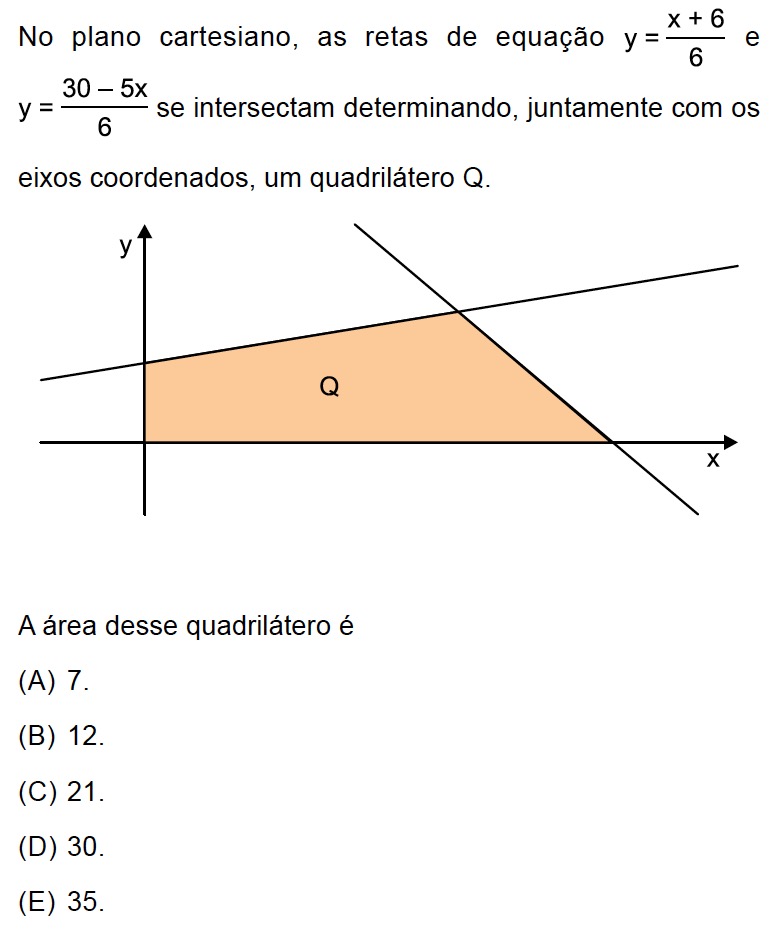
Considere a seguinte figura:

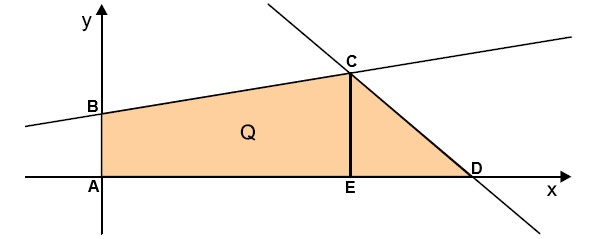
O ponto B é o ponto em que a reta de equação y =  intersecta o eixo y. Assim, se x = 0, tem-se y = 1 e B = (0, 1).

O ponto D é o ponto em que a reta de equação y =  intersecta o eixo x. Assim, se y = 0, tem-se 0 =  ⇔ x = 6 e D = (6, 0).

O ponto C é o ponto em que as duas retas se intersectam. Então:

Logo, C = . Além disso, A = (0, 0) e E = (4, 0).

A área do quadrilátero Q pode ser obtida somando-se as áreas do trapézio ABCE e do triângulo CDE.

Portanto, a área do quadrilátero é 7.