a) A partir da irradiação espectral no nível do mar, dada a constante expressa por , a potência por unidade de área
é:
A partir da expressão acima, o maior valor de ocorre para o maior valor de λ, ou seja, para a cor vermelha.
b) A potência da radiação que atinge a água pode ser determinada por:
Substituindo os valores fornecidos:
∴ P = 960 W
Entretanto, apenas dessa potência é absorvida pela água.
Assim,
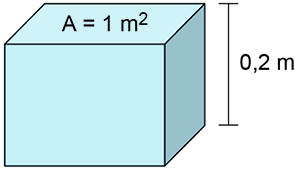
O volume da água contida na faixa mencionada no enunciado é V = 1·0,2 = 0,2 m3.
Uma vez que a densidade da água do mar é 1000 kg/m3, a massa de água contida nesse volume é 200 kg = 2·105 g.
Aplicando a definição de potência média:
Fazendo as devidas substituições numéricas:
∴ Δθ = 3,6 °C
c) A potência que atinge a superfície da água é 960 W. Assim, a energia que atinge essa superfície é dada por:
∴ ΔE = 960 J
A partir da equação fornecida, a energia de um fóton é:
Assim, o número de fótons (n) contidos em 960 J pode ser encontrado a partir da seguinte relação:
∴ n = 3,84·1021
