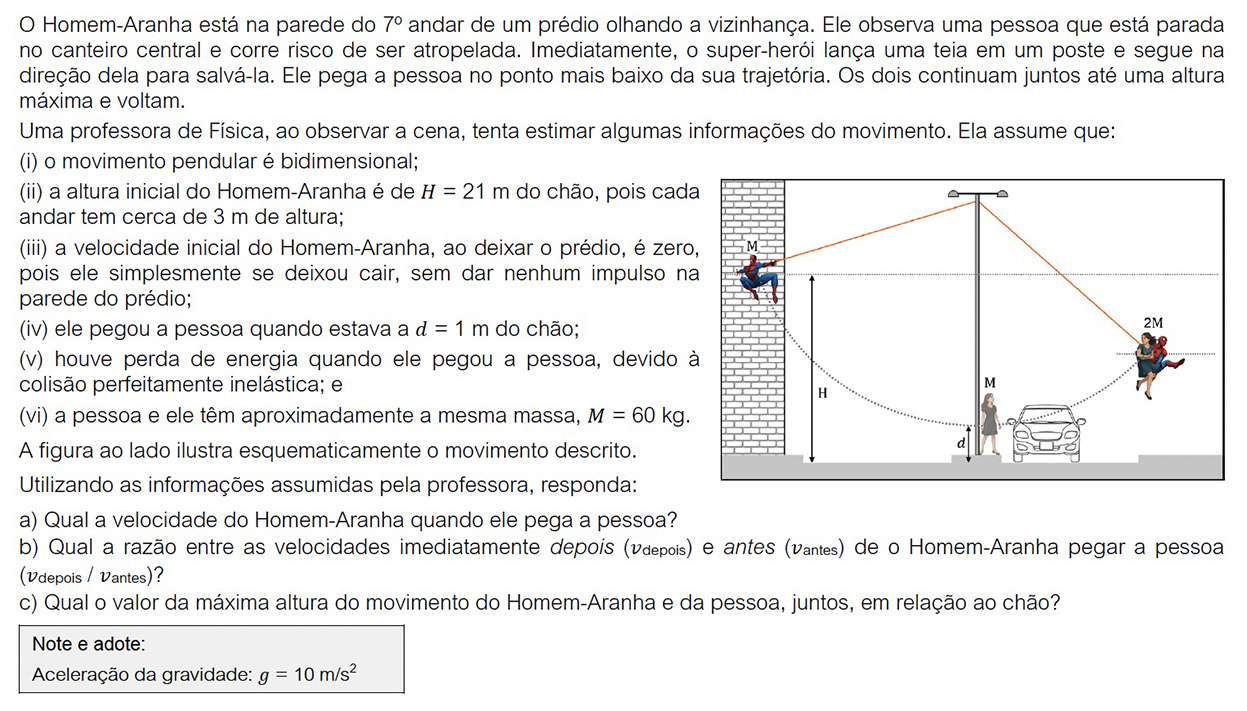
Na situação descrita ocorreram três eventos, (1) a descida do Homem-Aranha, (2) a colisão do Homem-Aranha com a pessoa e (3) a subida do sistema formado pelo Homem-Aranha e pela pessoa. Cada imagem a seguir representa o início e o final de cada um dos eventos.

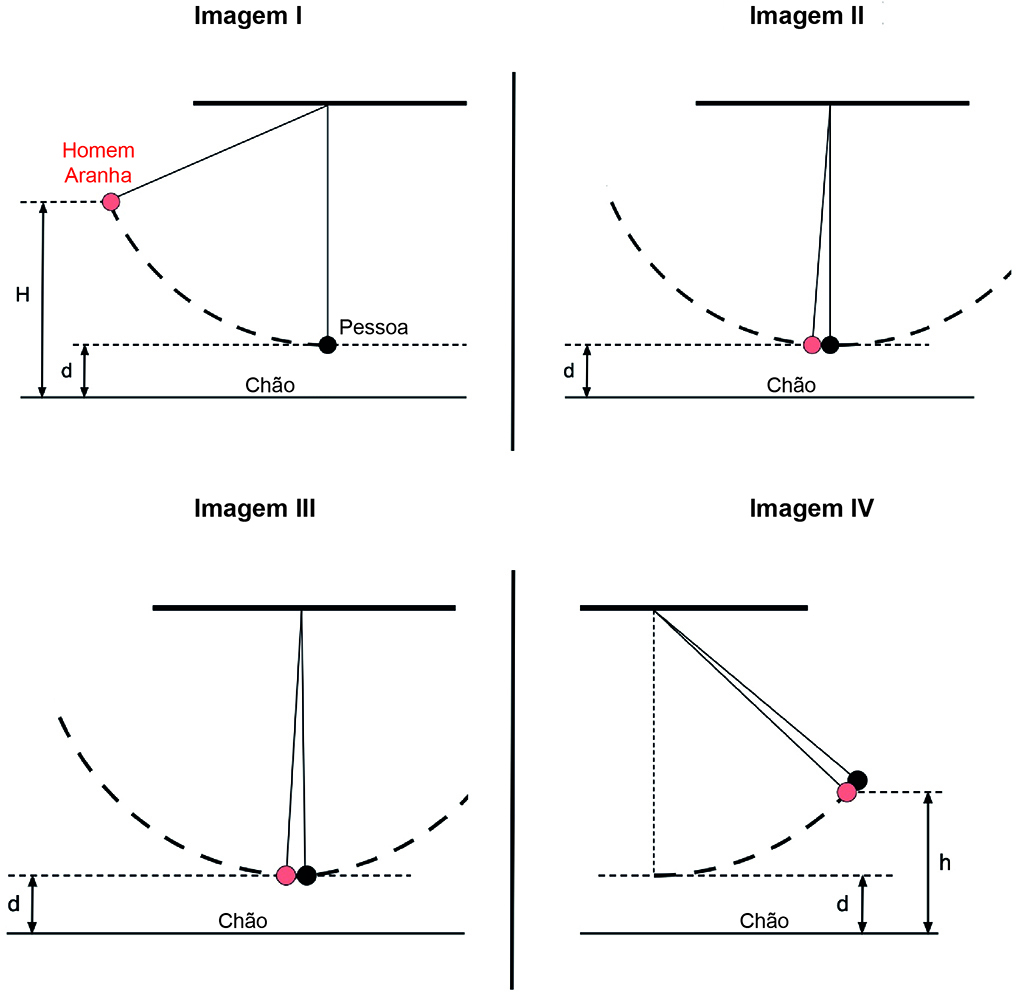
Da Imagem I até a Imagem II: Descida do Homem-Aranha;

Da Imagem II até Imagem III: Colisão;

Da imagem III até imagem IV: Subida do sistema de corpos.

a) Admitindo que a energia mecânica do Homem-Aranha se conserve quando ele vai da situação representada na Imagem I para II.

(E_m)_I = (E_m)_II

m_HA·g·(H - d) =  m_HA·(V_HA)_II²

10·(21 - 1) = (V_HA)_II²

∴ (V_HA)_II = 20 m/s

b) Os corpos que colidem da forma como descrita no enunciado constituem um sistema isolado, logo:

(Q_sist.)_II =(Q_sist.)_III 

m_HA·(V_HA)_II = m_HA·(V_HA)_III + m_P·(V_P)_III          (1)

Como a colisão foi perfeitamente inelástica,

(V_HA)_III = (V_P)_III          (2)

Logo, substituindo (2) em (1):

m_HA·(V_HA)_II = m_HA·(V_HA)_III + m_P·(V_HA)_III ⇒ m_HA·(V_HA)_II = 2·m_HA·(V_HA)_III

(V_HA)_II = 2·(V_HA)_III

c) Admitindo que a energia mecânica do sistema formado pelo Homem-Aranha e pela pessoa conserve quando ele vai da situação representada na Imagem III para IV.

(E_m)_III = (E_m)_IV

m_sist·g·(h - d) = m_sist.·(V_HA)_III²

10·(h - 1) = (10)²

∴ h = 6 m