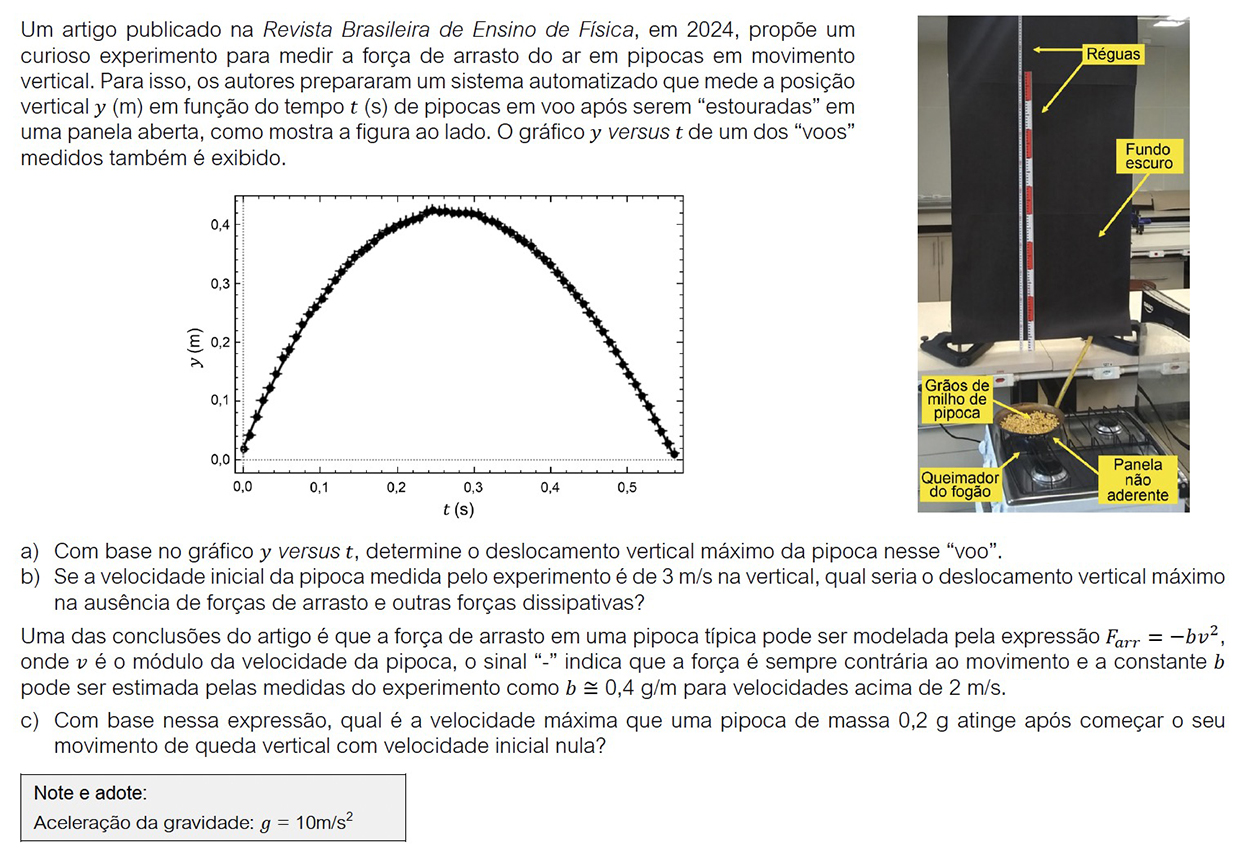
a) Observando-se o gráfico fornecido, verifica-se que a pipoca parte da posição y_i = 0,02 m, em t_i = 0, e atinge a posição máxima y_f = 0,42 m, como ilustrado a seguir.

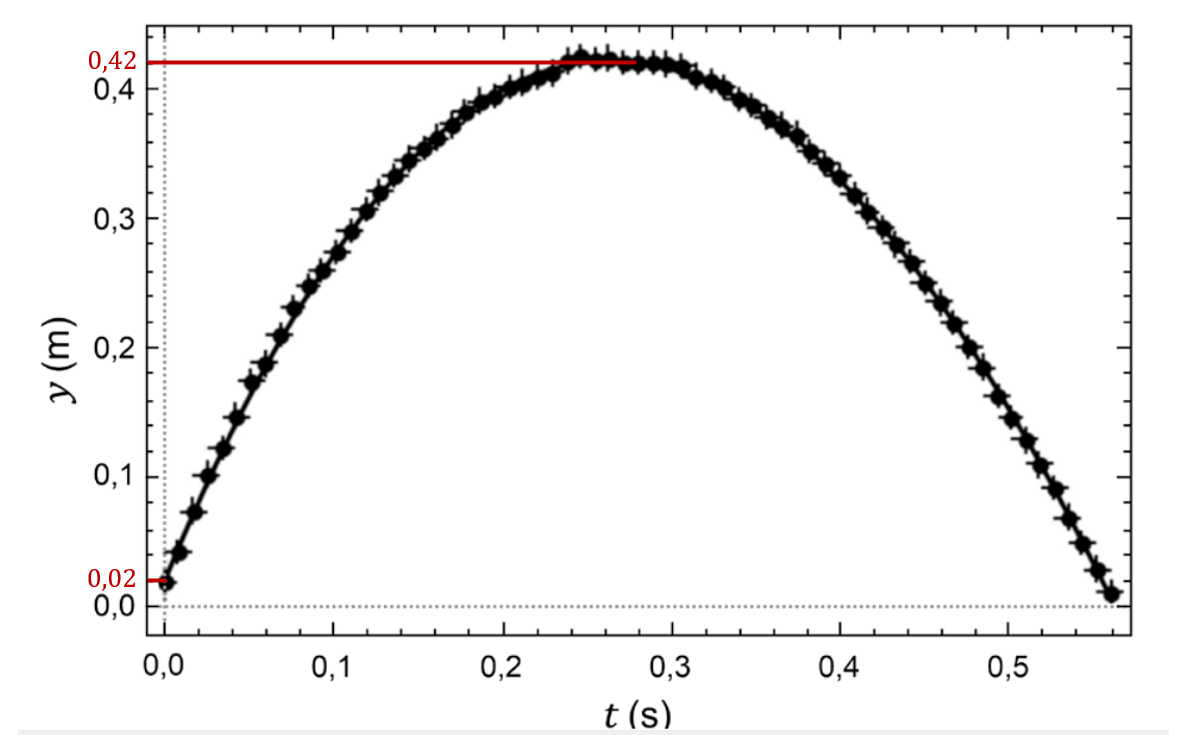
Logo, o deslocamento vertical máximo é:

b) Na ausência de arrasto e outras forças dissipativas, a única força aplicada na pipoca durante a subida é o seu peso. Logo, o módulo da aceleração da pipoca ao longo desse movimento será .

Como, no ponto mais alto, a velocidade é nula, temos que v = 0. Orientando-se a trajetória para cima, temos ainda que v₀ = 3 m/s e a = - 10 m/s².

Substituindo-se esses valores numéricos na equação de Torricelli, podemos obter o deslocamento máximo na ausência de arrasto e outras forças dissipativas, do seguinte modo:

c) De acordo com o enunciado, a pipoca é abandonada a partir do repouso. Nesse instante, a força de arrasto é nula e, portanto, a resultante das forças aplicadas na pipoca é o seu peso.

A partir desse instante, a pipoca acelera verticalmente para baixo. Como a força de arrasto aumenta de intensidade conforme a velocidade aumenta, a resultante, que corresponde à diferença entre o peso e o arrasto, diminui de intensidade conforme a pipoca se movimenta.

Em determinado instante, a resultante torna-se nula e a velocidade da pipoca é máxima:

Substituindo-se os valores numéricos fornecidos, no SI: