a) Com d = 1, temos . Se y = 1, então devemos ter
e, portanto, x = 1 ou x = –1.
Resposta: (1,1) e (–1,1)
b) Com d = 2, temos . Se y = 2, então devemos ter
e, portanto,
, o que implica x = 4 ou x = –4.
O gráfico de f, bem como a reta y = 2, estão representados visualmente a seguir:
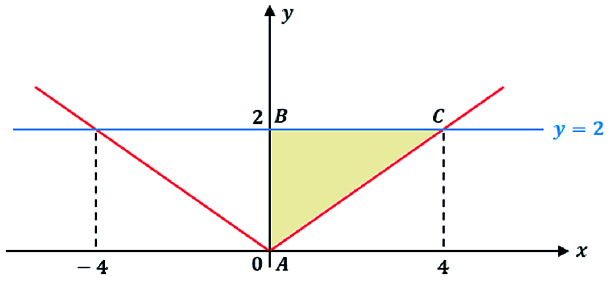
A área pedida é a área do triângulo ABC, que vale .
Resposta: 4
c) Se y = d, então devemos ter e, portanto,
, o que implica
ou
.
O gráfico de f, bem como a reta y = d, estão representados visualmente a seguir:
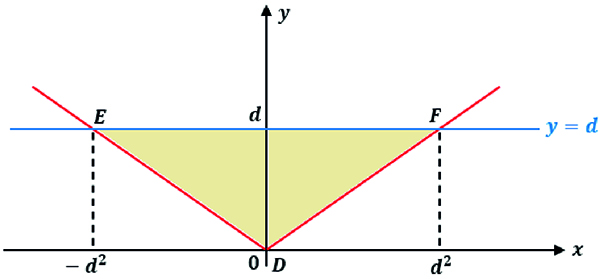
A área pedida é a área do triângulo DEF, que vale .
Resposta:
