a) Observe o triângulo PQA, em destaque na figura a seguir.

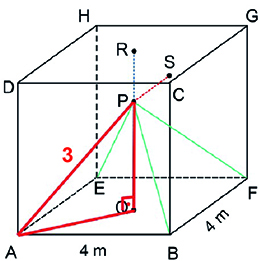
O segmento  tem metade da medida da diagonal do quadrado ABFE; assim,  m. Chamando de d a distância, em metros, da luminária até o chão, então, pelo Teorema de Pitágoras:

 

b) No caso em que as arestas laterais da pirâmide formam um ângulo de 45° com o chão, o triângulo PQA é isósceles.

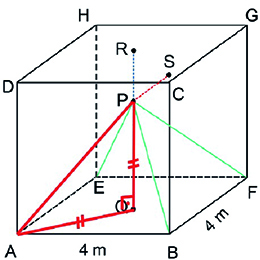
Assim, . Chamando de x a medida, em metros, da aresta lateral da pirâmide, então, pelo Teorema de Pitágoras:

 

c) Seja Q’ a projeção ortogonal do ponto Q no quadrado EFGH. A projeção da aresta  no plano EFGH é o segmento .

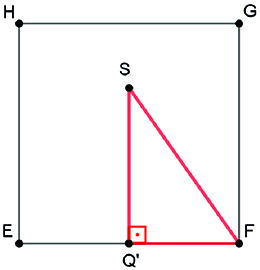
Como  m. Além disso, como Q é o centro do quadrado ABFE, Q’ é o ponto médio da aresta  e  m. Chamando de y a medida, em metros, do segmento , então, pelo Teorema de Pitágoras no triângulo SFQ’:

 

Obs.: Destacamos a imprecisão do enunciado ao informar que a pirâmide está inscrita no cubo, uma vez que seu vértice não toca a face superior.