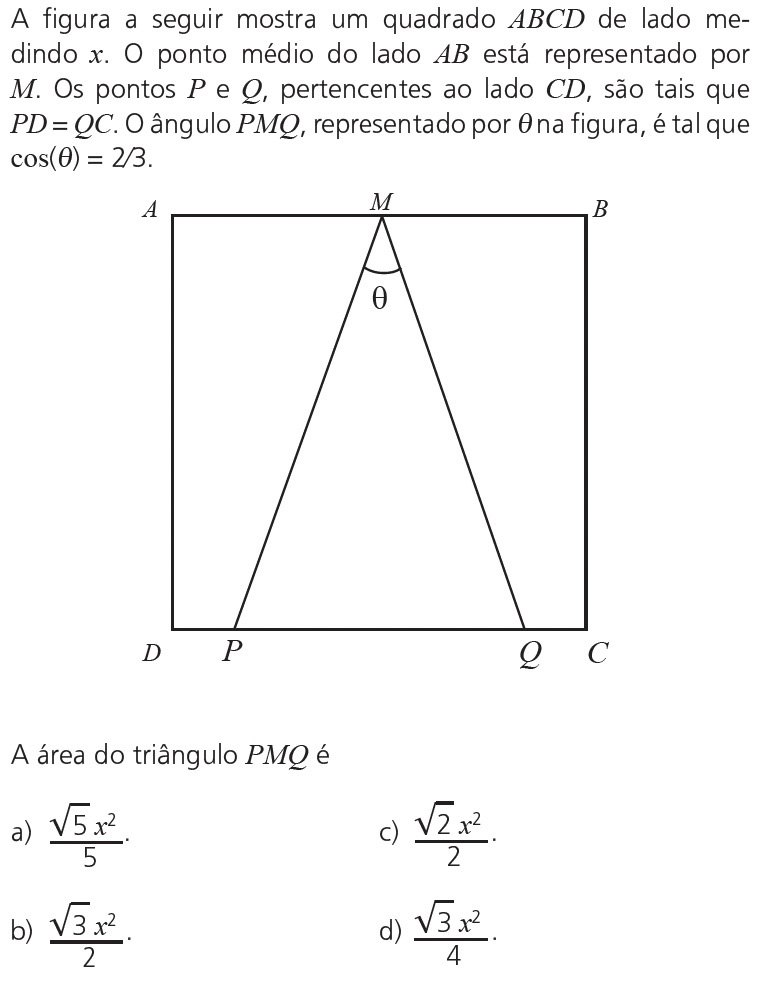
1ª solução:

Considere a figura a seguir, com as medidas assinaladas, e as linhas vermelhas verticais paralelas ao lado  do quadrado:

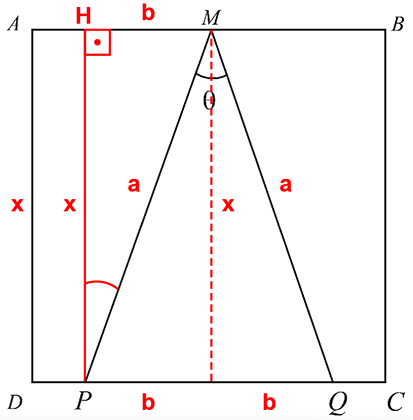
Aplicando o teorema dos cossenos no triângulo MPQ, vem:

Aplicando o teorema de Pitágoras no triângulo retângulo HPM:

Substituindo (I) em (II):

A área do triângulo MPQ é dada pela metade do produto entre a base de medida PQ = 2b e a altura correspondente x. Logo:

 

2ª solução:

Considere a figura a seguir, com as medidas assinaladas, e as linhas vermelhas verticais paralelas ao lado  do quadrado:

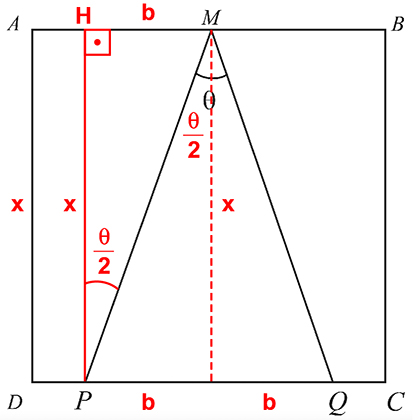
Como  e lembrando que , então:

Da Relação Fundamental, vem que . Logo,  e, portanto,  (I).

No triângulo retângulo HPM, tem-se  e, assim,  (II).

De (I) e (II), tem-se .

A área do triângulo MPQ é dada pela metade do produto entre a base de medida PQ = 2b e a altura correspondente x. Logo: