Um triângulo tem o menor lado medindo k cm, e as medidas de seus ângulos internos estão na proporção 1 : 2 : 3. A área desse triângulo, em função de k, é igual a:
- a
.
- b
.
- c
.
- d
.
- e
.
Se as medidas dos ângulos internos estão na proporção (1, 2, 3), podemos dizer que os ângulos internos do triângulo serão: (k, 2k, 3k). Sabendo que a soma dos ângulos internos do triangulo é 180º, temos:
k + 2k + 3k = 180º → 6k = 180º
Logo, os ângulos internos do triângulo são: 30º, 60º e 90º conforme a figura abaixo
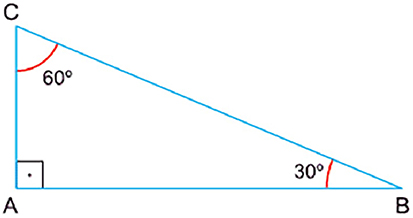
Se AC = k cm (O menor lado da figura), temos que:
Assim, a área (A) do triângulo ABC será: