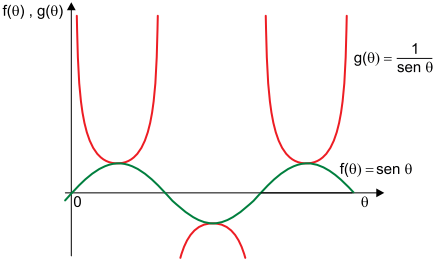
a) Da relação fundamental da trigonometria, temos que , ou seja:

b) O enunciado apresenta uma imprecisão. Na raiz do enunciado (antes do item a), define-se . Porém, no item b, encontramos .

Essa imprecisão pode induzir os candidatos a algumas interpretações erradas. Por exemplo:

• entender que é necessário resolver a equação  (a qual não tem solução)
• entender que foi pedido o valor mínimo de , que seria igual a –1

Dada a estrutura da questão, é razoável supor que a banca quis fornecer os gráficos das funções de leis  e , porém errou ao denominar uma delas novamente por . No entanto, pensando do ponto de vista do candidato, dadas as possíveis diferentes interpretações, não é razoável exigir essa conclusão, de modo que consideramos esse item como sem resposta.

Apenas a título de curiosidade, admitindo que essa era a intenção da banca, vamos prosseguir com a resolução.

Considerando apenas o trecho do gráfico em que , temos a figura a seguir, em que a notação  usada erroneamente foi substituída por :

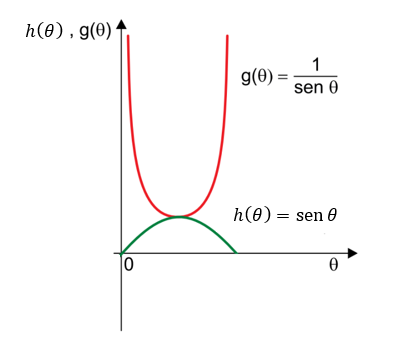
Com essa nova notação, temos que .

Pela figura, podemos notar que  para , caso em que . Além disso, para valores de  inferiores ou superiores a ,  se aproxima cada vez mais de zero e  cresce indefinidamente.

Ainda da figura, observando as curvaturas dos gráficos, é possível estimar que, à medida que  se afasta de ,  se aproxima de zero mais lentamente do que  cresce.

Resumindo:

•  para 
• se  se afasta de , a parcela  fica maior que 1 mais rapidamente do que a parcela  fica menor que 1, de modo que a soma das duas parcelas resulta em um número maior que 2

Dessa forma, podemos estimar que o valor mínimo de  é igual a 2.

Ainda a título de curiosidade, poderíamos obter uma solução exata usando um teorema bastante conhecido na Matemática: dados dois números reais positivos x e y, temos que a média aritmética entre eles é sempre maior ou igual à média geométrica desses números, sendo que a igualdade ocorre apenas se x = y.

Em linguagem algébrica, temos:

Considerando  e , os quais são positivos se , temos:

Note que o primeiro membro da desigualdade é justamente , ou seja, podemos garantir que . Por fim, como a igualdade só ocorre se x = y, ou seja, se , que ocorre apenas para , podemos concluir que o menor valor de  é 2, ocorrendo para .