Um lago artificial tem a forma de prisma reto, cuja base é o polígono UNIFESP, com UN = UP = 6 m, NI = PS = 2 m, IF = 1m, e ângulos indicados na figura.
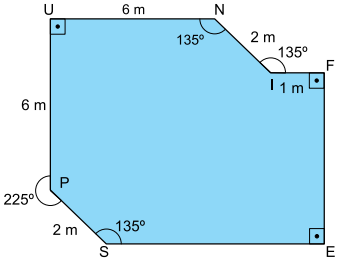
a) Calcule as medidas de , ambas em metros.
b) Calcule a altura aproximada do lago, em centímetros e com uma casa decimal depois da vírgula, sabendo que o volume do lago é igual a .
a) Inicialmente, note que são paralelas as retas que contêm os lados ,
e
,assim como são paralelas (e perpendiculares às anteriores) as retas que contêm os lados
e
.
Veja a figura a seguir, em que foram destacados dois triângulos retângulos isósceles:
- BSP, sendo B o ponto dado pela interseção das retas que contêm os lados
e
- AIN, congruente a BSP
Nesses triângulos, foram destacadas as medidas x dos catetos.
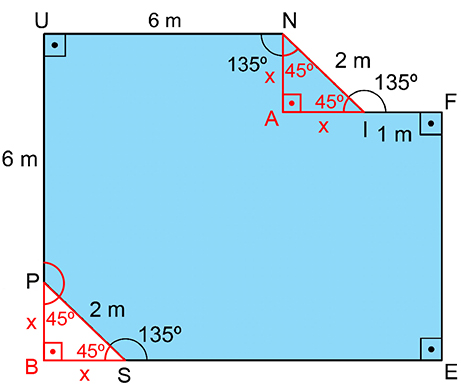
Como as retas que contêm os lados e
são paralelas, devemos ter:
Da mesma forma, como são paralelas as retas que contêm os lados ,
e
:
b) Como o volume do prisma é determinado pelo produto entre a área de sua base e a sua altura, precisamos determinar a área do polígono UNIFESP.
Veja a figura a seguir, que foi construída retirando-se o triângulo AIN de sua posição e sobrepondo-o ao triângulo BSP:
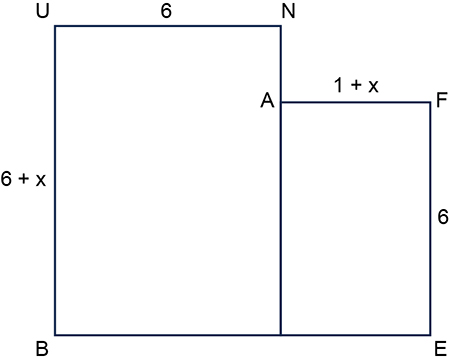
Como os triângulos AIN e BSP são congruentes, essa figura é equivalente (ou seja, tem a mesma área) ao polígono UNIFESP.
Para calcular sua área, é necessário determinar o valor de x, que é a medida dos catetos dos triângulos AIN e BSP:
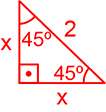
Do teorema de Pitágoras, temos:
Dessa forma, podemos calcular a área do polígono UNIFESP somando as áreas dos dois retângulos da figura acima:
Por fim, como o volume do lago é , denotando sua altura por H, temos:
Calculando uma aproximação de 1 casa decimal, temos que a altura do lago é de, aproximadamente, 16,7 cm.