Uma plataforma de streaming oferece os seguintes planos de pagamento para os consumidores dos seus filmes:
Plano I – o cliente paga inicialmente uma taxa de anuidade de R$ 286,00, e haverá pagamentos posteriores de R$ 9,00 por filme que assiste;
Plano II – o cliente não paga taxa de anuidade, mas terá que pagar R$ 16,50 por filme que assistir.
Considerando o período de um ano dos planos I e II,
a) determine sob qual condição de uso o Plano I é mais vantajoso para o cliente que o Plano II.
b) determine sob qual condição o gasto total com o Plano I excederia, em reais, o quadrado do número de filmes assistidos.
a) Denotando por n a quantidade de filmes assistidos, por P1 o valor pago (em reais) no Plano I e por P2 o valor pago (em reais) no Plano II, temos:
Para que o Plano I seja mais vantajoso, devemos ter , ou seja:
Como n deve ser um número inteiro, é necessário que . Dessa forma, o Plano I é mais vantajoso desde que pelo menos 39 filmes sejam assistidos.
b) Devemos ter:
Considerando que é a lei de uma função quadrática f, podemos esboçar seu gráfico a partir de sua concavidade (que é para cima, dado o coeficiente positivo do termo n2) e suas raízes. Para determinar essas raízes, devemos resolver:
Calculando o discriminante , obtemos:
Dessa forma, as raízes são:
Esboçando o gráfico de f, chegamos a:
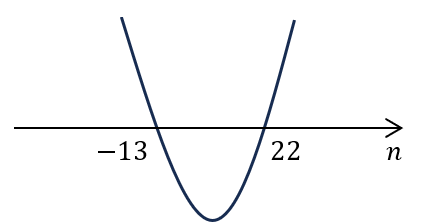
Dessa forma, podemos concluir que (ou seja,
) se
. Como n deve ser um número inteiro não negativo, devemos ter: