Uma amostra de gás ideal pode ser levada de um estado inicial A para um estado final C segundo a transformação ABC ou segundo a transformação ADC, indicadas no diagrama P × V. Sabe-se que a temperatura dessa amostra gasosa no estado A é TA = 450 K, que a transformação AD é isotérmica e que, na transformação BC, o gás recebeu 1250 J de calor de uma fonte externa.
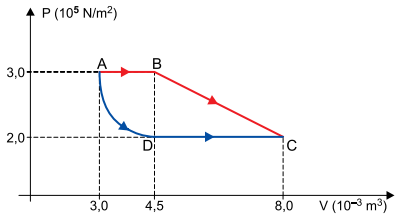
Calcule, para essa amostra de gás:
a) a temperatura, em kelvin, no estado C e a variação de energia interna, em joules, na transformação AD.
b) a variação da energia interna, em joules, na transformação BC.
a) A quantidade de gás não é alterada. Assim,
Substituindo-se adequadamente os valores:
A transformação AD é isotérmica, e, consequentemente, a energia interna do gás não muda, já que ela é diretamente proporcional à temperatura. Dessa forma, UA = UD. Assim,
b) O trabalho das forças de pressão ao longo da transformação BC pode ser obtido a partir da área sob o segmento BC, até o eixo das abscissas (eixo dos volumes):
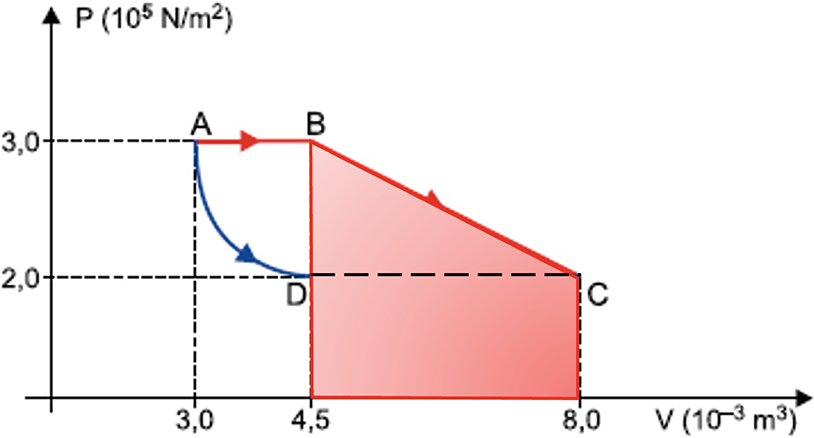
Como a figura é um trapézio:
Aplicando-se a primeira lei da termodinâmica, observando-se que QBC = + 1250 J: