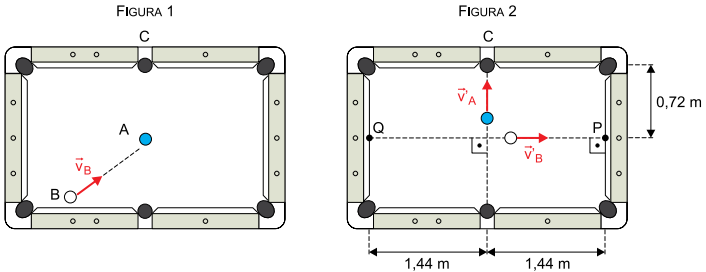
Em uma partida de sinuca, a bola branca (B) é lançada com velocidade vB = 3 m/s contra a bola azul (A), inicialmente em repouso (vA = 0), no centro da mesa, conforme a figura 1. Após a colisão, as bolas movem-se perpendicularmente uma a outra, com velocidades constantes , conforme a figura 2, e a bola azul cai na caçapa C.
Admita que as massas das bolas são iguais, que nessa jogada o atrito é desprezível e que todas as colisões são perfeitamente elásticas. Calcule, em segundos, o tempo para que:
a) a bola branca atinja o ponto P, indicado na figura 2, após sua colisão com a bola azul. Em seguida, calcule o tempo para que a bola branca percorra a distância PQ, indicada na figura 2, após sua reflexão no ponto P.
b) a bola azul caia na caçapa C, após ser atingida pela bola branca.
a)
- Após a colisão, a bola branca percorre uma distância de
com velocidade constante
. Logo, o intervalo de tempo decorrido nesse deslocamento pode ser determinado pela definição de velocidade média, como segue:
- A colisão da bola branca com a tabela é perfeitamente elástica. Desse modo, sua velocidade após a colisão continuará sendo, em módulo, igual a
b) A colisão entre as bolas A e B é um sistema mecanicamente isolado. Logo, intensidade da velocidade da bola A após a colisão pode ser determinada pela conservação da quantidade de movimento do sistema, da seguinte maneira:
Como a bola azul A estava inicialmente em repouso:
O esquema vetorial correspondente a essa expressão encontra-se representado a seguir:
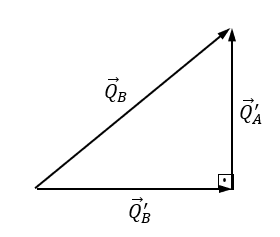
Logo, aplicando-se o teorema de Pitágoras:
Como todas as bolas têm a mesma massa:
Substituindo-se os devidos valores numéricos:
Logo, o intervalo de tempo decorrido no deslocamento até a caçapa C pode ser determinado pela definição de velocidade média, como segue: